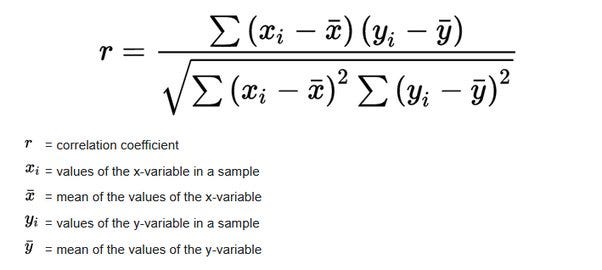A Complete Guide to Correlation Analysis 📊
Decoding Correlation: Importance, Common Pitfalls, and Illusory correlation
Hello, data-driven and curious minds, welcome to the 18th edition of DataPulse Weekly.
Each newsletter promises a journey through the fascinating intersections of data, stories, and human experiences. Whether you're an analyst or simply curious about how data shapes our world, you're in the right place.
Now, let’s dive straight into today’s Data Menu -
Today’s Data Menu 🍲
📊 Case Study: Correlation Analysis
🧠 Cognitive Bias: Illusory Correlation
📊 Case Study: Correlation Analysis
In the real world, multiple metrics are often intertwined, and understanding these relationships is crucial for making informed decisions. Let’s explore some real-world scenarios:
Does an increase in brand marketing spending impact sales?
Is there a relationship between higher delivery time and customer satisfaction scores?
Can the amount of time spent on Instagram affect sleeping hours?
Does posting frequently on LinkedIn increase followers?
How do we quantify these relationships? Enter Correlation Analysis.
Correlation Analysis helps determine the degree of relationship between two metrics, typically continuous ones like sales vs. spending or delivery time vs. satisfaction scores.
Performing correlation analysis should be your first step in understanding the connection between two metrics. It’s straightforward and quick.
What is Correlation and How is it Calculated?
Correlation analysis quantifies the relationship between two variables. It focuses on two key elements:
Strength: How strong is the relationship between the two metrics?
Direction: Is the relationship positive or negative?
We measure the strength and direction using a statistical measure known as the correlation coefficient.
Calculating the Correlation Coefficient:
Here's the formula (though you don't really need to remember it):
Let's examine sample data for Brand Marketing Spend and Sales. Calculating the correlation coefficient in Excel is straightforward using the ‘CORREL’ formula. You can also calculate it using SQL, Python, and other tools.
We have a Correlation of +0.47. First, let's clarify what this does not mean.
Common Pitfalls in Understanding Correlation:
A +0.47 correlation coefficient doesn’t mean that a $0.47 increase in spending will result in a $1 increase in sales or vice versa.
It also doesn’t mean that sales will increase 47% of the time with an increase in spending.
The Correlation Coefficient simply explains how strongly or loosely two variables are related. The correlation coefficient ranges from -1 to +1.
Here’s a general guideline for interpreting the magnitude of correlation coefficients:
Here are scatter plots showing different correlation strengths:

So, What is a Good Correlation?
The context and purpose of the analysis determine what constitutes a good correlation:
Context: In fields like marketing analytics, correlations between 0.3 and 0.5 can highlight important trends in consumer behavior. However, in areas like product testing, where accuracy is crucial, correlations of 0.7 or higher are usually needed to ensure reliability.
Purpose: For predictive modeling, such as sales forecasting, stronger correlations (closer to 1 or -1) are crucial. For initial data exploration, even moderate correlations can provide valuable insights and generate hypotheses.
Sample Size: In large datasets, like customer surveys with thousands of responses, even small correlations can be statistically significant. However, in small datasets, such as pilot studies with limited participants, only strong correlations are meaningful for drawing reliable conclusions.
Despite this, it's essential to remember that correlation does not imply causation.
Confounding variables can influence both variables being studied, leading to misleading correlations.
A confounding variable is an outside influence that affects both the independent variable and the dependent variable, leading to a false or misleading association between them. It can create the illusion of a cause-and-effect relationship where none exists.
Examples of Confounding Variables:
Ice Cream Sales and Shark Attacks:
Correlation: As ice cream sales increase, shark attacks also increase.
Confounding Variable: Temperature. Both ice cream sales and shark attacks increase during the summer when it’s warmer and more people are at the beach.
Chocolate Consumption and Nobel Prize Winners:
Correlation: Countries with higher chocolate consumption have more Nobel Prize winners.
Confounding Variables: Wealth and education levels. Wealthier countries tend to have better education systems and more resources, which can lead to more Nobel Prize winners, and they may also consume more chocolate.
Always remember, correlation doesn’t mean causation.
Conclusion:
When analyzing the relationship between two metrics, start with finding the correlation between them. Correlation indicates how strongly two metrics are related and whether the relationship is positive or negative. As a rule of thumb, a correlation greater than +0.5 or less than -0.5 is considered strong, but it depends on the context and purpose. A strong correlation means the two observations are highly related, but it doesn’t mean one causes the other.
Understanding correlation is crucial, but it's equally important to recognize a closely related bias – illusory correlation.
🧠 Cognitive Bias: Illusory Correlation
Did you know there are more than 180 ways your brain can trick you? These tricks, called cognitive biases, can negatively impact the way humans process information, think critically and perceive reality. They can even change how we see the world. In this section, we'll talk about one of these biases and show you how it pops up in everyday life.
Imagine you and your friends believe that every time you stay on the sofa without getting up during the match, your favorite sports team wins.
You've noticed that a few times when you stayed seated for the entire game, the team came out victorious. Because of this, you start thinking there's a special connection between staying on the sofa and the team's performance.
This belief that staying on the sofa during the match affects the outcome is an example of a cognitive bias called illusory correlation.
What is Illusory Correlation?
Illusory correlation is the tendency to perceive a relationship between two variables even when no such relationship exists. It's when people think that one thing causes another just because they happen to occur together, even though there is no real connection between them.
Other Examples Include:
1. Black Cats and Bad Omens: Many believe seeing a black cat brings bad luck. They remember unfortunate events following such sightings, despite no real connection between black cats and bad events.
2. Exam Performance and Breakfast: A student might think eating a particular breakfast cereal improves exam performance. They recall doing well after eating it, ignoring times they did poorly or succeeded without it.
3. Weather and Mood: People often believe rainy days make them sad. They remember feeling down on rainy days, overlooking other factors like personal experiences or lack of sunlight that affect their mood.
Tell us in the comments if you know of any illusory correlations.
People often see relationships between two things that aren't actually there. The sports team wins or loses based on their skills, practice, and competition, not because you stayed on the sofa.
Recognizing illusory correlations helps us avoid drawing incorrect conclusions from coincidental events.
That wraps up our newsletter for today! If you found this valuable, please consider subscribing and sharing it with a friend—it motivates us to create more content. Next time you hear someone making an incorrect conclusion from coincidental events, remember: correlation doesn’t imply causation, and beware of the illusory correlation.
Stay curious and connected!
Until next Tuesday!
Recommended Next Read: